课程目录
00.电子版资料
01.基础知识课—分式的基本概念与性质
02.迁移能力课—分式的运算与恒等变形
03.应用能力课——分式方程及应用
04.基础知识课—二次根式
05.迁移能力课—二次根式的化简
06.基础知识课——平移、旋转和轴对称
07.基础知识课—全等三角形（一）
08.模型方法课—全等三角形（二）
09.模型方法课—倍长中线与截长补短
10.基础知识课—垂直平分线与角平分线
11.基础知识课—等腰三角形
12.基础知识课—勾股定理及逆定理
13.模型方法课—全等三角形的经典模型（二）
14..模型方法课-全等三角形的经典模型（二）
15.迁移能力课–全等三角形证明与应用
16.【测评课】模型方法课—将军饮马问题
春下讲义
—
——————————————–
！！！！！！！！！！！！！！！！！！！！！
以下内容与本视频课程无关，
仅是AI对视频课程目录的总结，可以无视。
！！！！！！！！！！！！！！！！！！！！！
——————————————–
本课程内容丰富，涵盖了代数和几何多个重要知识点，具体如下：
代数部分
分式
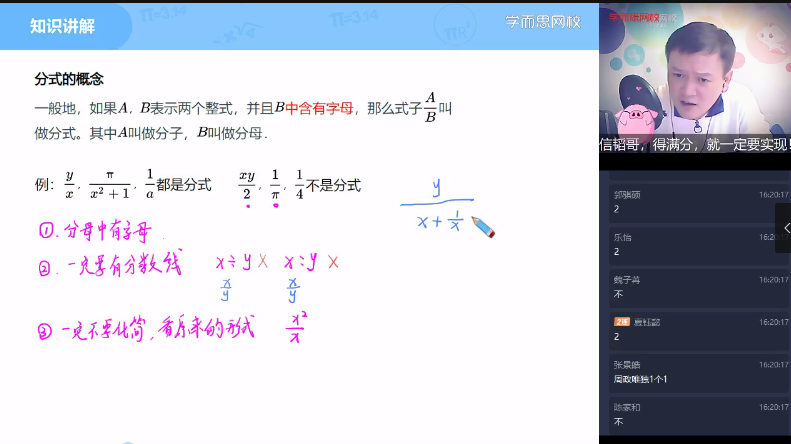
分式的基本概念与性质：是分式学习的基础，会介绍分式的定义，形如
B
A
（
A
、
B
是整式，
B
中含有字母）的式子叫做分式。还会讲解分式有意义、无意义和值为零的条件，以及分式的基本性质，即分式的分子与分母同乘（或除以）一个不等于
0
的整式，分式的值不变。
分式的运算与恒等变形：包括分式的加、减、乘、除、乘方运算，需要掌握通分、约分等技巧来进行运算。恒等变形则要求能根据分式的基本性质，将分式变形为不同的形式以满足不同的计算需求。
分式方程及应用：分式方程是分母里含有未知数或含有未知数整式的有理方程。学习分式方程的解法，关键是要通过去分母将其转化为整式方程求解，同时要注意验根。在应用方面，会涉及到行程问题、工程问题、销售问题等实际场景，通过建立分式方程模型来解决问题。
二次根式
二次根式：主要学习二次根式的概念，形如
a
（
a≥0
）的式子叫做二次根式。还会探讨二次根式有意义的条件，以及二次根式的性质，如
(
a
)
2
=a
（
a≥0
），
a
2
=∣a∣
等。
二次根式的化简：要求掌握二次根式的化简方法，如将被开方数中能开得尽方的因数或因式开出来，化为最简二次根式。同时，会学习二次根式的乘除法则
a
⋅
b
=
ab
（
a≥0,b≥0
），
b
a
=
b
a
（
a≥0,b>0
），以及加减法运算时的合并同类二次根式。
几何部分
图形变换与三角形基础
平移、旋转和轴对称：平移是在平面内将一个图形上的所有点都按照某个方向作相同距离的移动；旋转是在平面内把一个图形绕某一点旋转一个角度；轴对称是如果一个图形沿着一条直线对折后两部分完全重合。需要掌握它们的定义、性质和判别方法，这些变换不改变图形的形状和大小，只改变图形的位置。
全等三角形（一）：会介绍全等三角形的基本概念，如能够完全重合的两个三角形叫做全等三角形，以及全等三角形的对应顶点、对应边、对应角。还会讲解全等三角形的性质，即全等三角形的对应边相等，对应角相等。
全等三角形（二）及经典模型：深入学习全等三角形的判定方法，包括 “边边边”（SSS）、“边角边”（SAS）、“角边角”（ASA）、“角角边”（AAS）、“斜边、直角边”（HL）。模型方法课会涉及全等三角形的经典模型，如手拉手模型、一线三垂直模型、一线三等角模型等，通过模型的学习能快速找到全等三角形的条件，解决复杂的几何问题。
倍长中线与截长补短：这是两种重要的证明线段关系的辅助线添加方法。倍长中线是延长中线，使所延长部分与中线相等，再连接相应的顶点，构造全等三角形；截长补短是在较长线段上截取一段等于较短线段，或延长较短线段使其等于较长线段，从而证明线段之间的和差关系。
垂直平分线与角平分线：垂直平分线的性质是线段垂直平分线上的点到线段两端点的距离相等；角平分线的性质是角平分线上的点到角两边的距离相等。要掌握它们的概念、性质、判定及画法，在几何证明和计算中经常会用到这些性质来构造相等的线段或角。
等腰三角形：学习等腰三角形的定义，有两条边长相等的三角形叫做等腰三角形。还会探讨等腰三角形的性质，如两腰相等，两底角相等，顶角的平分线、底边高线和底边中线三线合一；以及等腰三角形的判定方法，如根据定义，有两条边相等的三角形是等腰三角形，或者有两个角相等的三角形是等腰三角形3。
勾股定理及逆定理：勾股定理指在直角三角形中，两条直角边的平方和等于斜边的平方。其逆定理是如果一个三角形的三边
a
、
b
、
c
满足
a
2
+b
2
=c
2
，那么这个三角形是直角三角形。勾股定理是解决直角三角形相关问题的重要工具，在数学、建筑与工程、物理学等领域都有广泛应用2。
测评课 —— 将军饮马问题：这是一个经典的几何最值问题，利用轴对称变换的思想，将在直线同侧的两点转化为在直线两侧，再根据 “两点之间线段最短” 来求解最短路径。它在实际生活和物理光学等领域都有类似应用1。
